THROUGH FAIRY-TALES TO MATH IN THE LESSONS

1. Introduction

During the whole history of the existence of mankind, as N. Filips (Filip, 1997) writes, people have told one another fairy-tales. The papyrus, dated approximately back to 1700 B.C., disclose that Pharaoh Cheops, the builder of the Great Pyramid in Egypt, was fond of fairy-tales, and there is a surprising similarity of the fairy-tales, which have survived, with the fairy-tales of today.

Fairy-tales are found throughout the world. Many of them are very ancient because the same plots and their elements have survived in different cultures on all the continents. Every person in his lifetime has many times experienced the miraculous impact of fairy-tales on his imagination, mind and feelings. They are our intellectual heritage, which never become obsolete, but always captivate emotionally with their simplicity, imagery and deep philosophy. But we seldom reflect upon the content of fairytales, not only in their ethical aspect but also as a source of different kinds of knowledge, including the knowledge of mathematics. However fairy-tales are not so widely used in mathematics education in primary schools and preschools because there is not completely evaluated mathematics content in fairy-tales.

Fairy-tales in a simple conspicuously imaginary way reflect mathematical notions and connections. When listening to and reading fairy-tales everyone experiences in his imagination the adventures of the heroes of fairy-tales, different situations in which they find themselves, they observe what happens and remember the expressions the heroes use, the settlement of different situations. Each generation have their favourite heroes of fairy-tales. For some it is the Thumbling, the Thumbelina or the princess Nesmejana, for others it is Karlsons or the bear Winney the Pooh, for some others it is Harry Potter. These characters are so bright emotionally that their impact is lasting throughout one’s lifetime. Even statesmen interweave now and then a character of fairy-tales in their speeches. O. Ambainis (Ambainis, 1955) wrote in the introduction to the selection of fairy-tales in 1955 that fairy-tales can be divided into three kinds:

• fairy-tales of miracles;
• animal fairy-tales;
• domestic fairy-tales.

The analysis of the content of fairy-tales leads to the conclusion that all kinds of fairy-tales contain mathematical notions and connections, but they found a little more in fairy-tales of miracles. In them, for example, the father’s son walks down the road till he comes to the cross-roads. There he has to choose which road to take. If he turns to the right he will come across some events, if he turns to the left he will experience quite different events, but if he goes straight still other events will await him there. Thus the son is offered three conditions and he has to choose one of them. Here are given clearly seen figurative representations, which form the foundations of the theory of probability. Fairy-tales brightly reflect the interconnection between the size and measure there are used different measures – the thumb (The Thumbeling, the Thumbelina), an inch (Tom Thumb), the distance of a call, a three-step length, etc.

2. The role of fairy-tales in the child’s development

Fairy-tales are usually explained as being fancy prose, more seldom as poetry, compositions, which have mainly found their expression in fairy-tales. The typical character of the European fairy-tale is a poor, brave and resourceful hero or heroine, who come into wealth and well-being after many risky trials. The German fairy-tales collected by the Brothers Grimm, have been retold in numerous variants. The form of fairy-tales can be used to express ethical and literary ideas, as the Danish writer Hans Christian Andersen did it. The plots of Latvian fairy-tales are very much alike the fairy-tales of other European peoples. One of the most prominent collectors and arrangers is Anss Lerhis-Puškaitis (1859-1903). The fairy-tales published by him in 1891 are well-known to everyone. Professor P. Šmits has made a collection of fairy-tales and tales in fifteen volumes. It should be noted that in the introduction to this edition P. Šmits especially stressed the educational and teaching role of fairy-tales in the children’s development. In their time the Brothers Grimm named their collection of fairy-tales “Kinder-und Hausmärchen” (Children-and home fairy-tales), and it was done so for didactic aims. “Gesta Romanorum”, composed in the beginning of the 14th century and used by clergymen in their sermons was used for this purpose, too. Tatjana Zinkēviča-Jevstigņējeva (Zinkēviča-Jevstigņējeva, 2004) admits that fairy-tales have been used as an educational and learning means since ancient times. It is possible with the help of metaphors to give children knowledge, without pressing and moralizing, about life, the relations among people, different possibilities of how to live one’s life. Already in ancient times the grown-ups passed knowledge to the children through tales and fairy-tales, stories and legends. Our ancestors have encoded various life situations and potential modes of behaviour, as well as concrete knowledge, in the fairy-tales. These codes have survived up to our times and they help us comprehend the world around in interconnections.

The style of fairy-tales is simple they do not urge children to make immediate logical judgements and conclusions. Fairy-tales offer characters with the help of which children imperceptibly learn the information necessary for life. Fairy-tales are full of activities, events and changes following one another. The language and style of the fairy-tales are understandable for children. The language is simple, but at the same time promising secrets and miracles: "once upon a time in a certain country….", in olden times when birds and animals could speak, etc. Fairy-tales take children to a world of things, relations and conceptions, which in everyday routine often may remain unnoticed and they are unconscious of them. Fairy-tales make them look at, realize and comprehend them as if being observers. They prepare children for further perception of things and connections, which in their turn guarantee a successful beginning of learning at school and in their further life. The outstanding representative of humanitarian pedagogy V. Suhomļinskis (Suhomļinskis, 1974) has said once: ’I cannot imagine learning without listening to fairy-tales and composing them.’ Many educators, among them K.E. Vandergrift (Vandergrift, 2004) suggests using fairy-tales more actively in the study process. It is a means of developing a creative, educational and learning stimulating environment, by involving the children's imagination and asking them to interpret and explain the expressions and actions of the heroes of fairy-tales.

3. Expressions in fairy-tales characterizing mathematical notions

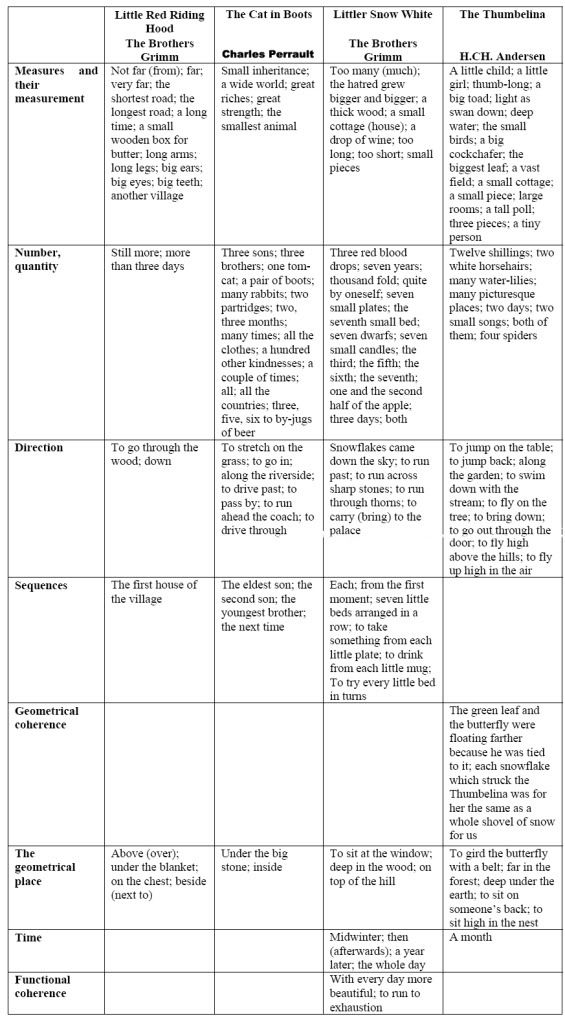
Fairy-tales are an excellent means in the acquisition of mathematical notions and connections, because they contain many significant parts of mathematics: the basic notions of arithmetic, algebra, geometry, numerical theories, the theory of probability and others. Four fairy-tales, best known for generations, were chosen for the theoretical analysis – Little Red Riding Hood, Tom Cat in High Shoes, Little Snow White and the Thumbelina.

Picture 1.: Math nations in a fairy – tales

The Latvian fairy-tale “Bear-ears” gives a more detailed analysis of the reflection of the notion of "group". Here three kinds of group can be mentioned: group with a definite number of elements, group of numberless elements and group which contain no elements (empty group).

Picture 2.: The notion of a set in the Latvian fairy–tale “Lāčausis” (Bear ears)

The expressions and the development of the plot of the fairy – tale can be arranged according to mathematical sections. The set is seen in situations when the youngest son has there horses and he uses them by turns, or when the blind feel the parts of the elephant and thus form the notion of the elephant. The number theory is seen in the frequent use of clichés connected with the number ‘three’: three brothers; instead of the three heads of the dragon, when cut off, crop up three on each head; at the other end of the world (miles and miles away); twelve robbers; the young girl walks through all the three rooms one after the other. Functions or functional coherence is seen in situations illustrating the fact that the shorter the hero of the fairy – tale the braver he is, or also in the conclusion that the less you mention the evil the sooner you will benefit something.

Elements of geometry find their expression in the descriptions of objects and phenomena in fairy – tales: a crooked club; a steep hill; an inch – tall little man; to travel around the sea; to walk all over the kingdom, i.e. crosswise and criss–cross. Foundations of analytical geometry are found in the description of situations showing the activities of the characters of fairy – tales: to dash upright; to sink downright in the ground: to fly over slantwise; to cast a glance at the person sitting opposite; to fall on one’s back; to follow one’s shadow.
Elements of the theory of probability are seen in situations when the son of the father is standing at the crossroads and he has to choose one event put of the three offered by choosing a road.

4. Teachers’ Points of View on the Mathematical Notions in Fairy-tales

A poll of 86 teachers was carried out to clarify their points of view concerning the mathematical notions found in fairy – tales, which can be used for the learners’ comprehension. The teachers’ opinions were that the learners can acquire the following mathematical notions:

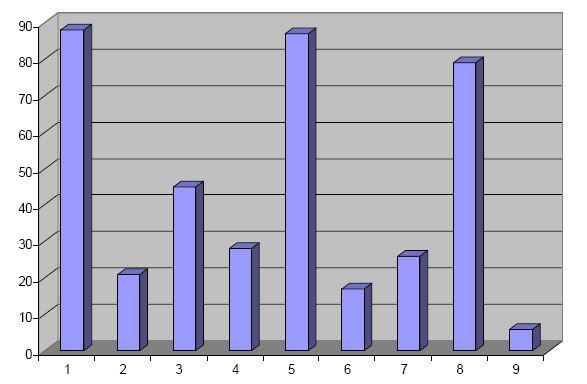
Picture 3.: Teachers’ Points of View on the Mathematical Notions in Fairy-tales

Legend:

1) differentiate between the following notions: one, many (much), one by one, no one, more, fewer (less), more than, less (fewer) than;
2) make up rows of numbers in growing and diminishing order;
3) name the numerals;
4) divide objects into two parts and in halves;
5) determine objects according to their size: long (tall), short, wide, narrow, high, low, thick, thin, the longest, the shortest, the widest, the narrowest, etc.;
6) use different measures and measure different objects;
7) define directions in space;
8) name the parts of twenty – four hours;
9) identify geometrical forms and figures.

Most teachers acknowledge that fairy-tales can be used best of all when learning to differentiate between the notions one, many (much), one by one, no one, more, fewer (less), more than (less than) (88%), and when learning to determine objects according to their size: long, short, wide (broad), narrow, high, low, thick, thin, the longest, the shortest, wider, narrower, etc. (87%). The number ofteachers who see the importance of fairy-tales when teaching children to name the parts of twenty-four hours is a little smaller (78%). Less than half of the respondents (45%) mark out the usefulness of fairy-tales when learning to name the ordinal numerals which seems a little surprising as the numerals first, second, third are often used in fairy-tales. Only 6% of the respondents consider it necessary to use fairy-tales for the identification of geometrical forms and figures. It should be mentioned that comparatively seldom these geometrical notions are used in fairy-tales. However, the teachers see the usefulness of fairy-tales when learning to make up rows of numbers in growing and diminishing order (21%), to divide objects into two parts and to have them (28%), to use different measures and measure them (17%), to define directions in the room (26%).

5. Conclusion

Consequently, fairy-tales include a number of notions which help children get mathematical notions about the surrounding world, its variety and glory. Fairy-tales not only develop children’s imagination but also develop their skills to use mathematical connections and basic notions in a simple understandable language in primary and preschools mathematics education, at the same time putting stress on these connections and so paving the way to further serious acquisition of the systemic course of mathematics.

It is advisable to use fairy – tales for the development of the learner’s comprehension of mathematical notions. It can be done in various ways. Here are some of them:

• by drawing the learner’s attention to particular mathematical notions or coherence, and encouraging them to find similar ways of expression in other fairy – tales;
• by asking the learners to compose fairy – tales of their own, making use of definite mathematical notions and coherence;
• by encouraging the learners to illustrate situations in fairy – tales, which refer to mathematical notions and coherence

For example, when asking the children to make up a fairy-tale about three small frogs, a high hill and descending it, or asking the children to recall which fairy-tales tell us about two sisters or three brothers, or asking the children to draw the flight of the Firebird slantwise across the sea.

In this investigation is more analyzed content of fairy-tales for mathematics education. In futures investigations could be particularly analyzed efficiency fairy-tales using for achievements of children in mathematics lessons.

Literature

[1] Ambainis, O., Feldhūne, A. (1955) Latviešu tautas pasakas. Izlase. Rīga.: Zinātņu akadēmijas izdevniecība, 5. – 15.lpp.
[2] Philip, N. (1997) The Illustrated Book of Fairy Tales. London: Dorling Kindersley Limited.
[3] Suhomļinskis, V. (1974) Sirdi atdodu bērniem. Rīga: Zvaigzne.
[4] Šmits, P. (1937) Ko pasakas un teikas māca? – www.ailab.lv (15.10.2008.)
[5] Vandergrift, K.E. ( 2006) Snow White Teaching. – www.scils.rutgers.edu (12.05.2008.)
[6] Zinkeviča – Jevstigņējeva, T. (2004) Pasaku terapija audžuģimenēs. Psiholoģijas pasaule. 2004.Nr3, 5.- 8.lpp.

Author Rudite Andersone, Dr.paed., professor, University of Latvia, Riga, Latvia
(http://dppd.ubbcluj.ro/adn/article_2_2_13.pdf)